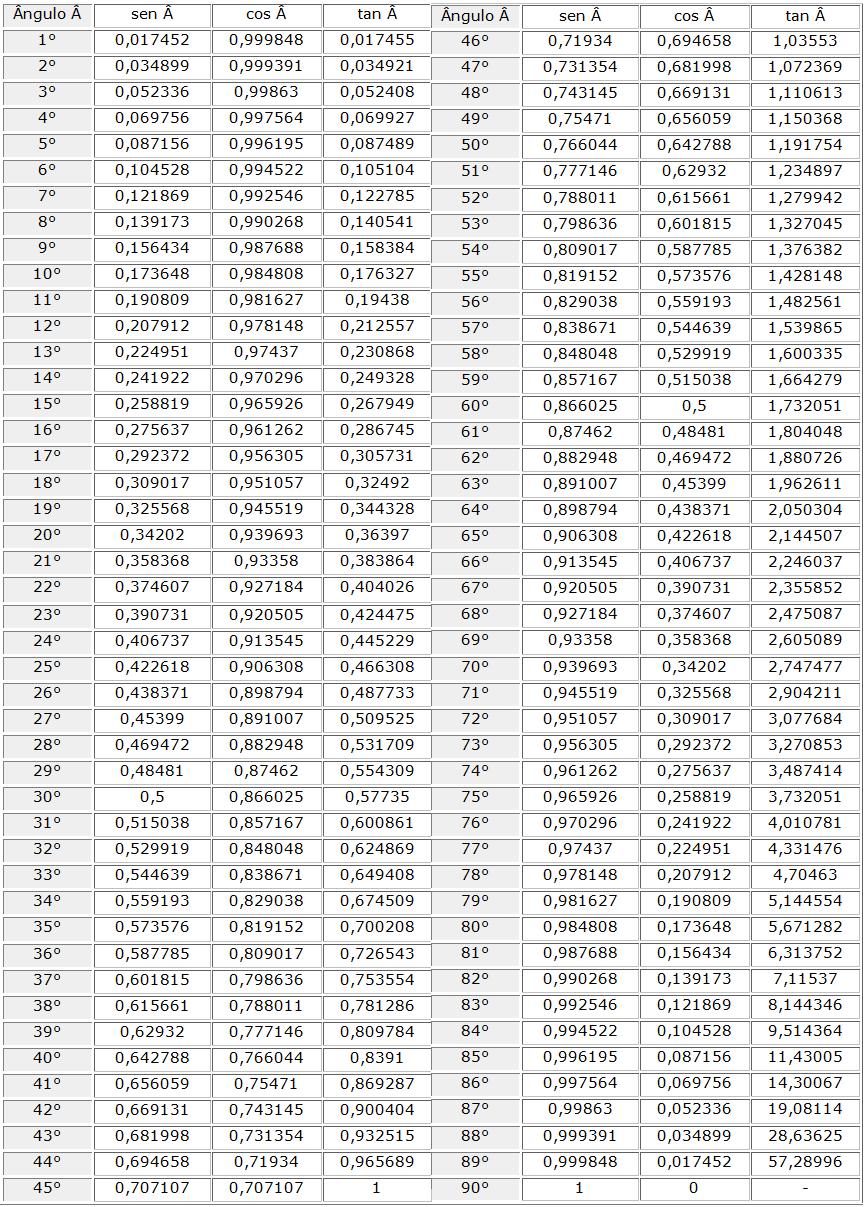
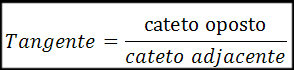Arquivos Fórmula - Brasil Blogado

julho 25, 2014

Concentração molar ou molaridade – fórmulas e exemplos

Concdentração Molar ou da quantidade de matérias.

Para chegar a uma fórmula é necessário aprender antes, saber do que o assunto se trata, por isso vamos a uma breve explicação sobre o mesmo.

A Concentração molar ou molaridade é do que a quantidade de soluto, em mol, dissolvidos num volume de solução em litros. E o mol, para quem não sabe é a quantidade de substâncias de um sistema que contém unidades elementares e não podem ser especificadas por um átomo, molécula, íon, elétron, fóton ou por um grupo especifico.

Desta maneira a concentração em quantidade de matérias é chamada de “concentração em mol/l” ou“concentração em quantidade de matéria” e não concentração molar ou molaridade como muitos acreditam ser.

Agora vamos às fórmulas e aos exemplos, mas antes vá ao seu quarto e pegue a tabela periódica, será necessário tê-las em mãos.

Fórmulas e Exemplos

A fórmula geral é a seguinte:

M= Nº de mols do soluto

Nº de litros de solução

Porém, acontece de alguns casos não apresentar o valor da matéria do soluto, mas a massa apresentada vai ser expressa em gramas (m₁). E quando isso acontecer, é preciso encontrar a quantidade de matéria do soluto em mols (n₁) por meio da divisão da massa do soluto pela massa molar do próprio soluto.

n1= Massa do Soluto

Massa molar do soluto

Sendo, assim se substituir n₁ na equação, terá a seguinte fórmula:

M= m1

M1 V(L)

Agora colocando em prática por meio de um exemplo, ficará da seguinte maneira.

Exemplo:

Em uma solução aquosa encontra-se cerca de 100 mL de volume, no qual contém 20 g de NaCl. Como proceder para expressar a concentração dessa solução em quantidade de matéria por volume, ou seja, em concentração de mol?

Resolução:

A fórmula a ser utilizada é a mesma acima, porém o volume não está em litros e por isso deve fazer a conversão de unidades.

1 L —— 1000 mL
V —— 100 mL
V = 0,1 L

Além disso, é necessário descobrir o valor da massa molar, no caso do sal NaCl e E para que se consiga é preciso saber os valores das massas atômicas de ambos os elementos e realizar o cálculo da massa molar que ficará da seguinte maneira:

M (NaCl) = 1 . 23+ 1 . 35, 46

M (NaCl) = 58,46 g/mol

Agora sim, dá para substituir os valores da fórmula e descobrir qual é a concentração de mol por litro.

M= m1

M1 V(L)

M= 20 g

(58.46 g/mol). (o.1 L)

M= 3,4 mol/L

julho 23, 2014

Tabela seno cosseno tangente

Tome cuidado no momento de coloca-lo na fórmula.

O seno, cosseno e tangente é uma das áreas mais importantes da matemática, pois eles fazem parte da trigonometria, que abrange os estudos dos cálculos, sendo importante para área da física, topografia, engenharia, engenharia marítima e engenharia aérea.

Seno

Assim, como os outros, ele tem uma função na trigonometria, porém terá uma ação diferente. Deste modo, um triângulo retângulo com um de seus ângulos internos igual a θ, define-se Sen(θ) sendo a razão entre o cateto oposto a ” θ” e a hipotenusa deste triângulo. Ou seja:

Por exemplo: se um triângulo retângulo que a hipotenusa possui o valor de 10 e seus catetos são de valores 6 e 8. O seno do ângulo oposto ao lado de valor 6, vai ser de 6/10 , ou seja, 0,6.

Cosseno

O cosseno, também é uma função, dado um triângulo retângulo com os ângulos internos igual a θ, pode definir que cos θ como a proporção entre o cateto adjacente a θ e a hipotenusa do mesmo triângulo, sendo:

Verifique sempre as suas propriedades. — Cateto adjacente/ Hipotenusa = Cosseno. (Foto:Divulgação)

Tangente

Ela pode estar sendo colocada em três grupos, sendo eles:

* Geometria: vai ser quando uma reta toca em uma curva ou superfície, sem ter de corta-lá, fazendo com que ela compartilhe um único ponto com a curva.

Verifique o estilo de tangente que se pede. — Cateto Oposto/ Cateto Adjacente = Tangente. (Foto:Divulgação)

* Trigonometria: é a proporção entre o cateto oposto e adjacente a um dos ângulos agudos de um triângulo retângulo. Ou a função que relaciona os possíveis valores dos ângulos agudos do triângulo retângulo ao valor da tangente destes ângulos.

* Geometria Analítica: é um nome alternativo que se dá para o coeficiente angular de uma reta ou então, curva.

Enfim, todos eles precisam de uma tabela de identificação para saber quais os reais valores e ângulos. Sendo assim, a tabela que representa essas três ações está sendo mostrada na imagem abaixo:

Não se esqueça das fórmulas, de cada um para chegar aonde se pede. — Tabela de Seno, Cosseno e Tangente. ( Foto: Divulgação)

abril 6, 2014

Hidrostática: teoria e conceito de Arquimedes

Arquimedes de Siracusa é um dos físicos que apresenta uma das teorias mais interessantes em relação ao conceito da hidrostática, processo que também pode ser denominado como estática dos fluidos ou fluidostática. Mesmo sendo pouco conhecido em relação a sua vida, é considerado como um dos maiores cientistas da Antiguidade Clássica devido a sua ideologia e fundamentos.

A hidrostática é classificada como a parte física que estuda as forças exercidas por e sobre os fluídos que se encontram em repouso, onde a sua pressão é sempre perpendicular a superfície, podendo ainda variar a sua profundidade.

Fórmula geral da pressão

Hidrostática: teoria e conceito de Arquimedes. — Arquimedes de Siracusa.
(Foto: Reprodução)

P = pgh

Onde:

» P: pressão hidrostática (em pascals);
» p: densidade ou a massa específica da água (em quilogramas por metro cúbico);
» g: aceleração da gravidade (em metros por segundo quadrado);
» h: altura do líquido que se encontra geralmente por cima do traço (em metros).

Princípio de Arquimedes

Arquimedes afirmava que:

Um corpo sólido imerso num fluido, sofre a ação de uma força dirigida para cima, igual ao peso do fluido deslocado, isto é, devido a pressão hidrostática do fluido.

Fórmula:

FE = Wfluido = ρfluido . Vdeslocado . g

Características do empuxo:

» Direção: vertical;
» Intensidade: será a mesma do peso do fluído que será deslocado pela presença do sólido;
» Sentido: de baixo para cima.

Exemplo:

Um barco tem o seu peso contra-balançado por uma força ou por um empuxo que é igual ao volume da água em que se desloca, correspondendo assim ao seu volume submerso. Caso mais pessoas forem colocadas no barco, o volume submerso irá aumentar, tal como a sua força de impulsão que permite com que ele flutue.

fevereiro 25, 2014

Aprenda como calcular a fórmula percentual de um composto

Ao ver o titulo de nosso tema, você deve ter ficado confuso, isso é normal. Muitas pessoas acham que se trata de matemática financeira, mas não é. Essa matéria se trata de química, sim.

Hoje iremos tirar algumas duvidas, como por exemplo: calcular o percentual de um composto. Mas primeiramente precisamos saber o quê ela significa.

A fórmula pode estar ser chamada de Percentual ou então de centesimal. E para quem não sabe, essa fórmula é de suma importância, pois é por meio dela que se determina outras fórmulas químicas do composto. Sendo assim, é impossível obter as fórmulas: mínima, empírica e molecular, sem ela.

Ela tenta indicar que a massa de cada elemento químico presente em cem partes de uma atmosfera, possui uma porcentagem “X”, em cima dele. Ou seja, ela trabalha como se estivesse utilizando a matemática simples também, fazendo assim com que cada elemento da substância, possua uma quantidade “X” de elemento.

Tome cuidado para não colocar a quantidade diferente de cada elemento. — Fórmula de Percentual

Primeiramente é necessário saber que as substâncias puras possuem menos elementos combinados dentro da mesma proporção da massa. Por tanto, tome cuidado com a quantidade que irá colocar na fórmula. E para que possa compreender melhor o que estamos querendo lhe demonstrar, vamos á um exemplo.

Exemplo:

Questão: determine a fórmula do percentual de um sal inorgânico, sendo que a análise da amostra indica que em 50 gramas dessa substância possui cerca de 20 gramas de cálcio.

Atenção: a resolução de cada massa vai ter de ser feita por um cálculo diferente, porém sempre com a mesma fórmula. Por tanto ela vai ficar da seguinte maneira:

Massa do cálcio = massa do cálcio na amostra . 100%
massa total da amostra

Porcentagem de massa do cálcio = 20 g . 100%
50 g

Porcentagem de massa do cálcio = 40 %

Sendo assim, logo a fórmula centesimal pode ser representada por: Ca_40%

É bem simples aplicar a fórmula da porcentagem quando já se tem as quantidades adequadas de cada elemento. Procure sempre estar indo em busca da quantidade, para depois resolve-la. No mais, não esqueça manter a concentração no que está lendo e fazendo.

outubro 21, 2011outubro 22, 2011

Fórmula de Watts

A eletricidade é muito importante nos dias de hoje, pois com ela está toda a tecnologia existente, do que adiantaria toda essa modernidade sem o recurso energético, as instalações são realizadas em casas, prédios, postes das ruas, quando uma instalação é mal feita podem acontecer problemas como curtos circuitos, explosões.

Ohm – unidade de resistência – um ohm é a resistência oferecida à passagem de um ampéres quando impelidos por um volt.

Ampéres – unidades de corrente – um ampéres é a corrente que um volt pode enviar através de uma resistência de um ohm.

Watt– Unidade de energia elétrica ou energia um watt é o produto de um ampéres e um volt um ampere de corrente que flui sob a força de um volt dá um watt de energia.

Volt ampéres – produto de volts e ampéres, como mostrado por um voltímetro e amperímetro em sistemas de corrente contínua o ampére volt é o mesmo que watts ou a energia entregue em sistemas de corrente alternada o volts e ampères podem ou não ser 100% síncrona quando síncrona os volts-ampéres é igual ao watts em um wattímetro quando não exceder síncrona ampères volt watts -potência reativa

Ampéres quilovolts – um ampéres quilovolts – KVA – é igual a 1.000 volts-ampéres.( Fonte: www.engineeringtoolbox.com).

Exemplo de calcular Watts:

Potência em watts = (corrente em amperes) x resistência ao quadrado em ohms.

Encontrar = Watts.

Quando volts e amp éres são conhecidos.

Potência (Watts) = VOLTS x Amperes

Temos um pequeno servidor com uma placa de identificaçãomostra 2,5 ampères. Dado um normal de 120 volts, 60 hz fonte de alimentação ea leitura ampères do equipamento, faça o seguinte cálculo:

Potência (Watts)= 120 * 2,5 RESPOSTA: 300 WATTS.

Fonte citada: http://www.abrconsulting.com