Tag: carnaval

Publicado em

Quantos dias depois do carnaval é a pascoa

O Carnaval é uma festa tradicional no Brasil onde toda a população se reúne em meio as cores e muito samba para comemorar. E já a páscoa é a celebração cristã que celebra a morte e ressurreição de Cristo. Apesar de não ter sido esse o dia de sua ressurreição. E como as duas festas são próximas, muitas pessoas ficam na dúvida sobre a quantidade de dias que devem esperar para que a páscoa aconteça. 

Cálculo da Páscoa

O Dia da Páscoa, por definição, é o primeiro Domingo após a lua cheia, que acontece após o equinócio vernal que pode cair entre 22 de Março e 25 de Abril. E tal seqüência que foi elaborada para os dias de Páscoa, vem se repetindo em ciclos de aproximadamente 5.700.000 anos e para que se chegue a estes ciclos, são utilizados fórmulas que mostra o “Cálculo Eclesiástico” que segundo a história só foi definido em 325 com o Concílio de Nicea. 


 O Carnaval sempre há de acontecer 47 dias antes da Páscoa. Logo então, ele pode cair entre as data 04 de fevereiro ou  9 de março. E já o Corpus Christi, que é a celebração do corpo de Cristo, acontece 60 dias após da Páscoa. Logo ele pode acontecer de 21 de maio até 24 de junho. Por tanto, um vai estar sempre antecedendo o outro. 

Fórmula de Gauss

A fórmula de Gauss é uma das mais utilizadas para somar os dias que antecede a páscoa. Vejamos então, como ela funciona.

Nela o ANO deve ser introduzido com 4 dígitos e o operador MOD é o resto da divisão. Tal fórmula vale para os anos de 1901 a 2099, porém pode ser estendida para os mais anos, caso seja alterado X e Y, conforme a tabela pedir. 

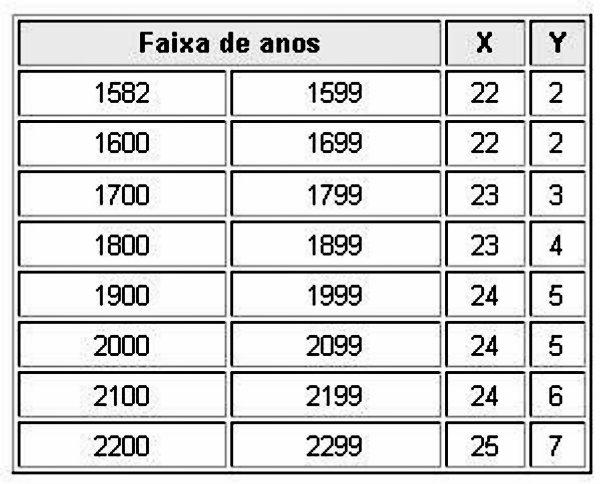
Utilize a fórmula para saber a data do ano que deseja saber.
Tabela utilizada na fórmula de Gauss.
(foto:divulgação)

Vejamos um exemplo de como se usar a fórmula. 

Ano de 2015:

a= 2015 MOD 19 = 1

b= 2015 MOD 4 = 3

c= 2015 MOD 7 = 6

d= (19 * 1 + 24) MOD 30 = 13

e= (2 * 3 + 4 * 6 + 6 *13 + 5) MOD 7 = 1

(d + e) = 13 + 1 = 14

Sendo assim:

. Domingo de Páscoa é 05/04/2015
. Carnaval: 17/02/2015
. Corpus Christi: 04/06/2015

Publicado em

Tema da vencedora do carnaval do RJ 2014

O Carnaval teve inicio na  Grécia, porém chegou aos brasileiros através dos europeus.

 E foi no meio dos donos de terreiros e boêmios, que tinham gosto pela alegria e diversão, meio a qualquer pessoa, que surgiu o carnaval que vemos hoje.

A Unidos da Tijuca, mantém como cores representantes o azul e o amarelo.
Bandeira da escola de samba Unidos da Tijuca.
(Foto Reprodução)

Mas, não vamos falar disso, vamos além. Iremos abordar sobre a vencedora do desfile das escolas de samba do estado do Rio de Janeiro. A escola de samba, Unidos da Tijuca, invadiu a praça da Apoteose, com o enredo e tema: Acelera Tijuca. A escola homenageou um dos maiores ídolos de todos os tempo, Ayrton Senna.

A Unidos da Tijuca foi a grande  campeã do Grupo Especial das escolas de samba do Rio de Janeiro. Para se sagrar-se campeã, ela obteve  299,4 pontos, rendendo-lhe o terceiro título, em um intervalo de cinco anos apenas.

Dentre as escolas de samba do grupo especial, a Unidos da Tijuca foi a última a desfilar, por volta das quatro horas da manhã e terminou às cinco e trinta e seis, da terça feira. E nesse tempo ela mostrou 3 mil e 600 componentes em 34 alas. Entrou em cena todos os desenhos que representavam a corrida automobilística e grandes ídolos já imortalizados como Ayrton Senna.

E devido a isso, era possível ver um filme nostálgico se passando meio ao brilho dos olhos de cada um que estava presente ali. Imaginem, só vocês: o Speed Racer, Ligeirinho, Papa Léguas, Sonic, The Flash, Penépole Charmosa, Dick Vigarista e dentre outros. Pilotos e invenções do homem, em meio a Sapucaí.

Veja o quão rápido são os personagens apresentados pela escola de samba, campeã do ano de 2014, no Rio de Janeiro.
Não se trata apenas de desenhos, criações e ídolos, mas sim, de toda uma história.
(Foto Reprodução)

E para consagrar, tudo que estava ali, a rainha de bateria, Juliana Alves, não fez feio,  mostrou todo charme, exuberância e malemolência que uma brasileira tem. E para acompanha-lá, os integrantes da bateria, se fantasiaram de mecânicos, o que por sua vez, mostrou a todos que qualquer um pode conseguir concertar os erros, que já causou.

Ela mostrou ao público o bom somba no pé e o porque de ter sido escolhida por seus colegas de escola.
Madrinha de bateria, Juliana Alves- Foto Reprodução

Enfim, o que realmente mais emocionou o público, foi a homenagem feita ao corredor de fórmula 1, Ayrton Senna. Eles mostraram ao público a sua trajetória, desde o início até a sua morte. E mais, mostraram á todos o quão sábio e veloz ele era e a falta que ele fez e faz nestes vinte anos de ausência. Mas presente na memória de todos os brasileiros.

Por meio desse tema, eles tentaram mostrar que a pressa pode ser inimiga da perfeição, mas que, se feita com agilidade e da maneira correta, pode-se chegar aonde nem se imagina. No caso deles, a vitória e respeito de muitos.
Acelera Tijuca, era o tema principal da escola de samba.
( Foto Reprodução)

 

 

Publicado em

História do Carnaval

O entrudo (atual carnaval) chegou ao Brasil em meados do século XVII, a comemoração festiva teve uma grande influencia das festas carnavalescas que ocorriam na Europa, principalmente em países como a França e a Itália, onde a comemoração acontecia em formas de desfiles urbanos, e os carnavalescos geralmente usavam fantasias e máscaras.

Em meados do século XIX, começaram a surgir os primeiros blocos carnavalescos, os “corsos” e os cordões no Brasil. As pessoas/carnavalescos se fantasiavam, improvisavam a uma decoração para os seus carros e em grupos os mesmos iam para as ruas da cidade desfilar (essa é a origem dos carros alegóricos, que nos dias atuais são típicos das escolas de samba).

Em meados do século XX, o carnaval foi tomando expansão se tornando então uma festa popular. O crescimento da comemoração carnavalesca se deu principalmente pela popularidade das marchinhas, pois as mesmas tornavam o carnaval cada vez mais animado.

A primeira escola de samba brasileira surgiu no Rio de Janeiro, a escola de samba se chamava Deixa Falar (atual Estácio de Sá), a mesma foi criada por Ismael Silva um popular sambista carioca. Á partir dai o carnaval urbano começou a ganhar um novo formato, surgindo então novas escolas de samba na cidade do Rio de Janeiro e na cidade de São Paulo. E também nas cidades de Recife e de Salvador.

Publicado em

Feriado carnaval de 2012

 

O carnaval é uma festa que ocorre no mês de fevereiro ou março, em 2012 será no dia 21 em uma terça-feira, uma data onde o Brasil recebe muitos turistas devido à grande movimentação que a data traz, muitas cidades brasileiras são palcos da alegria do carnaval, escolas de samba criam carros alegóricos, fantasias para competir e se divertir.

A data em que se refere ao carnaval é considerado feriado nacional podendo ser variada todos os anos, todo o povo brasileiro recebe dispensa do trabalho, para participar ou assistir os desfiles de escolas de sambas de todo país, a festa de carnaval do ano de 2005 em Salvador foi reconhecida no Guines Book como a maior festa realizada em rua pública do país

É comum no carnaval o som alto vindo de trios elétricos acompanhados de vários artistas, os sambódromos ficam lotados todos em busca de muita diversão, o carnaval do Rio de Janeiro e São Paulo são os mais famosos devido aos desfiles das escolas de samba que se preparam o ano todo para competir entre as melhores escolas carnavalescas.

O Carnaval Brasileiro é uma das maiores festas populares e alegres do mundo, para quem quer aproveitar para viajar para as principais cidades do país é necessário se programar com antecedência, pois nesta época do ano os hotéis ficam lotados, e os aeroportos também, planeje antes para evitar transtornos, aproveite o carnaval pule e dance bastante.

Publicado em

PACOTES BARATOS PARA O CARNAVAL 2018

O Carnaval é uma festa vibrante e alegre, e que é comemorada em vários lugares do Brasil e do mundo, é uma época em que algumas pessoas buscam lugares com alegria carnavalesca e muita animação e é claro um bom samba. O Brasil é um dos países onde o carnaval é bem conceituado e animado, ressaltando que o carnaval brasileiro tem fama mundial, no entanto na época do carnaval, mas precisamente no mês de fevereiro turistas do mundo inteiro escolhem as vibrantes cidades brasileiras, para se divertir e se alegrar, encantar com o ritmo caloroso que é o samba, e quem sabe até mostrar que tem samba no pé.

Como o carnaval é uma festa tipicamente brasileira, muitas cidades no Brasil oferecem uma ampla estrutura voltada as comemorações carnavalescas. Próximo ao mês em que o carnaval ocorre no Brasil, a busca por pacotes baratos para o carnaval aumentam significativamente nas agencias de turismo, e os roteiros brasileiros são os mais diversificados. Os pacotes baratos para o carnaval 2018 são encontrados nas agencias de turismo, nos mesmo são disponibilizados passagens aéreas de ida e volta, hospedagem com direito a café da manhã, e transfer do aeroporto ao hotel na chegada e na saída do mesmo.

Escolha uma das cidades brasileiras onde o carnaval é contagiante e divirta-se:

  • Salvador
  • Rio de Janeiro
  • São Paulo
  • Fortaleza
  • Recife
  • Natal
  • Porto Seguro
  • Caldas Novas
  • Aracaju
  • João Pessoa

Pacotes BARATOS para o CARNAVAL 2018:

Destino- Fortaleza
Pacote barato:
7 noites e 8 dias- á partir de R$1.068,00;
Destino-Natal
Pacote barato:
7 noites e 8 dias- á partir de R$1,039,90;

Destino- Porto Seguro
Pacote barato:
7 dias e 8 noites- á partir de R$599,90;
Destino- Fernando de Noronha
Pacote barato:
7 dias e 8 noites- á partir de R$989,00;

Destino- Recife
Pacote barato:
7 noites e 8 dias- á partir de R$3019,90;

Publicado em

PACOTES BARATOS PARA O CARNAVAL 2019

O carnaval é uma festa que reúne alegria, ritmo contagiante, e o famoso “jeitinho” brasileiro, muitas cidades no Brasil comemora essa festa tão esperada, ressaltando ainda que a mesma atrai pessoas do mundo inteiro, pensando nesses aspectos as agencias de turismo lançam para a venda pacotes baratos para o carnaval 2019, onde o cliente encontrara um leque em opções de cidades brasileiras.

Os pacotes baratos para o carnaval 2019, podem variar de valor, os mesmo irá depender da escolha da cidade, e dos tipos de serviços disponibilizados no pacote de carnaval. Como o roteiro é bem diversificado, e os tipos de serviços que podem ser requeridos também é diversificado, os valores dos pacotes baratos para o carnaval 2019 também são bem variáveis e acessíveis.


Pacotes BARATOS para o CARNAVAL 2019:

Tipo de pacote barato para carnaval 2019:
Destino- Rio de janeiro valor- R$3089,00
Hospedagem;
6 dias e 7 noites;
Café da manhã;
Passagem ida e volta;
Translado do aeroporto ao hotel na chegada;
Translado do hotel ao aeroporto na saída do mesmo;

Tipo de pacote barato para carnaval 2019:
Destino- Salvador valor- R$2098,00
Hospedagem;
7 dias e 8 noites;
Café da manhã;
Passagem ida e volta;
Translado do aeroporto ao hotel na chegada;
Translado do hotel ao aeroporto na saída do mesmo;

Tipo de pacote barato para carnaval 2019:
Destino- Fortaleza valor- R$1090,00
Hospedagem;
6 dias e 7 noites;
Café da manhã;
Passagem ida e volta;
Translado do aeroporto ao hotel na chegada;
Translado do hotel ao aeroporto na saída do mesmo;

Tipo de pacote barato para carnaval 2019:
Destino- Aracaju valor- R$ 989,00
Hospedagem;
6 dias e 7 noites;
Café da manhã;
Passagem ida e volta;
Translado do aeroporto ao hotel na chegada;
Translado do hotel ao aeroporto na saída do mesmo;